UNIDADE 4 - Portas Lógicas

Porta lógica AND

    Nesta porta, a saída apenas será 1 quando todas as entradas N forem 1 (verdade), ou seja se há 2 entradas, as 2 entradas precisam ser 1 (verdadeiras).

Circuito exemplo:

Tabela verdade:

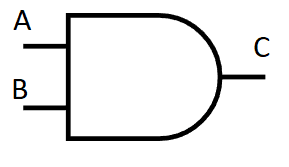
Representação gráfica:

Porta lógica OR

    Nesta porta, a saída será 1 caso qualquer uma das N entradas for 1 (verdade), ou seja, neste caso precisamos apenas de uma ocorrência, ou N > 0 ocorrências.

Circuito exemplo:

Tabela verdade:

Representação gráfica:

Porta lógica NOT

    Nesta porta, a saída é invertida de sua entrada, ou seja, caso a entrada seja 0 (falsa), ela se tornará 1 (verdadeira), e caso a entrada seja 1 (verdadeira), ela se tornará 0 (falsa).

    Esta porta também contem a condição de "suportar" apenas uma entrada, ou seja, podemos "inverter" apenas uma entrada.

Tabela verdade:

Representação gráfica:

Como poderemos ver ao combinar esta
porta com outras, o sinal que simboliza
esta "inversão" é o círculo a frente
da porta

Porta lógica NAND e NOR

    Estas portas representam a combinação da porta "NOT" com as portas "AND" e "OR", respectivamente, sendo assim, podemos dizer que sua saída será o inverso da saída OR ou AND.

NAND:

    Na porta AND, obtemos a saída 1 caso todas as entradas N sejam 1, sendo assim, temos apenas uma saída 1, mas agora, como precisamos inverter a saída do AND, o contrário será a saída com todas as N entradas 1 (verdadeiras) como uma saída 0 (falsa) e as demais como 1.

Tabela verdade:

Representação gráfica:

NOR:

    Na porta OR, obtemos uma saída 1 (verdadeira) caso qualquer uma das N entradas seja 1, assim, tínhamos apenas uma saída 0, no caso de todas as entradas N serem 0. Para a porta NOR, pegaremos estas saídas e as inverteremos, tendo como resultado uma saída 1 (verdadeira) apenas para o caso que todas as N portas sejam 0 (falsas), e as demais portas serão 0, como é visto na tabela a seguir.

Tabela verdade:

Representação gráfica:

obs: A maneira mais fácil de se obter a saída final é pegarmos a saída da porta lógica sem a inversão (AND ou OR) e depois invertermos todas as saídas, assim teremos a saída na porta NAND ou NOR.

Porta lógica XOR e XNOR

    Estas portas são denominadas exclusivas, sendo a Exclusive-OR (XOR) e a Not XOR (NXOR), é importante citar que esta operação só existirá entre 2 entradas. As portas possuem as seguintes condições:

XOR:

    Na porta XOR, obteremos uma saída 1 (verdadeira) somente se as duas entradas forem DIFERENTES, ou seja, caso elas sejam 0 e 1, ou 1 e 0, nos demais casos onde temos ambas as entradas como 1 ou 0, teremos uma saída 0.

Tabela verdade:

Representação gráfica:

XNOR:

    Como podemos imaginar, se tratando de uma inversão da porta anterior (XOR), nesta porta, teremos uma saída 1 (verdadeira), caso as 2 entradas sejam IGUAIS, e para os demais casos, agora será uma saída 0 (falsa).

Tabela verdade:

Representação gráfica: